Fractional Latitudes
Avebury's position
Whereas Stonehenge is significant for solar reasons, Avebury is astronomically aligned. Avebury also appears to be one of the ancient temples of the world positioned on exact longitudinal fractions.
Giza is unusual in that it is at 1/3rd (30 degrees) of the 90 degree quadrant (equator to pole).
Other notable sites appear at fractions of 1/7th of the 90 degree quadrant.
Thebes (in Egypt) is 2/7ths (25.7 deg)
Delphi is 3/7ths (38.5 deg)
What may come as a surprise is that Avebury is 4/7ths (51.42 deg) or 360/7
To be more exact, 360/7 is 51.42857142857143
The position of Avebury was the one that surprised me the most. Put that position in a geosite as the longitude and what do you get?
Avebury location
e.g.
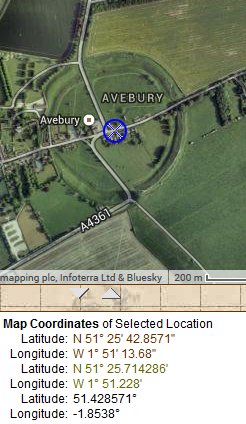
That is a real gob-smacker. Usually with my feeble attempts at staring at maps, alignments and meridians, places are fairly close, or quite close, or close enough. Avebury, however, is none of these. It is absolutely spot-on, to an astonishing degree of precision. Is this a wonderful curiosity, or a hidden mystery?
You might wonder (as I did) if any other locations in Britain seem to share this Fractional Latitudes phenomena. It's a bit hit and miss:
3/5 ths perhaps? (3/5 * 90 = 54.0)
Thornborough Henge: 54 12 N, 01 35 E
Newgrange: 53 42 N 6 29 E
Both within a few minutes of 54: (3/5ths) - but not precisely enough to be convincing?
Why bother?
From this distance in space and time, it's difficult to appreciate what the original purpose may have been. Or why 1/7th fractions would have been chosen in the first place.
As for my purpose, what I'm attempting to do is reverse-engineer some basic Megalithic Astro-Geometry. The original Megalithic Astro-Geometry Initiates (let's call them MAGI) understood triangular coordinates. Just as the original UK Ordnance Survey used triangulation to map the whole of the UK, I'm hypothesising that the MAGI would need to use the same method to establish some base stations for astronomy. The base stations do have to be far enough apart to maximise (for example) the difference in the maximum height of ascension of any astronomical object.
Why maximise the difference? One reason is measuring of the size of the planet. The greater the difference, the more accurate the measurement.
As we are mostly all Sleep Walkers (with a respectful hat tip to Arthur Koestler), stumbling in the dark, fumbling to understand what's gone before, I'm trying to take a systemic approach, and run the numbers down. Then we can see what fractional latitudes have been chosen, even if we don't know why. The spreadsheet below shows all the fractional latitudes from 1/3rds to 1/13ths. I've left gaps where a fraction is a duplication of an earlier one. For example, 2/6ths is the same as 1/3rd. Highlighted in yellow are a few locations found (so far).

For the sake of accuracy, I should mention that these are all in the Northern Hemisphere, but (in theory) there's no good reason why some similar sites might not be found in the Southern Hemisphere.
This page on Prehistoric Greece reminds me that:
The site of the Delphine Oracle, arguably the most important oracle in the classic world and sacred since prehistoric times, originally being a shrine to Gaia and a centre from which sacred temples and oracle centres were placed apparently according to principles of longitude. Delphi is also associated with the worship of Apollo (the sun god), who is said to have killed the serpent Python at Delphi, essentially supplanting one form of worship with another. The sites status as an Earth Navel was recognised by Herodotus, who connected the oracle centre at Delphi with the one at Karnak in Egypt. both sites at which Omphalos stones have been found.
Ref : Prehistoric Greece
Copyright © Ancient Wisdom website.
Delphi = 3/7ths, 38° 29' N
Karnak (Thebes) = 2/7ths, 25° 43' 0 N
Amarna, Akhetaten
Amarna
Akhetaten means "Horizon of the Aten" (disc of the sun)
27.6 deg latitude = 5/13ths
That would be a 5:12:13 triangle. Which should be familiar to anyone aware of Stonehenge's 5:12:13 geometry.
Another question : is 21/29ths a significant fraction?
21/29ths = 58.9655 deg north
That is within a megalithic stone's throw of the Standing Stones of Stenness and the Ring of Brodgar.
If you have any suggestions, please contact me.
Footnote
If you ask most folks in the UK where "our" decimal number system came from, the most common answer whould be "Arabic". In fact, the Arabs got the decimal number system from India. It maybe relevant that :
The earliest references to astronomy are found in the Rig Veda, which are dated to c.2000 BC. Some Vedic notices mark the beginning of the year and that of the vernal equinox in Orion. This was the case around 4500 BC. Yajnavalkya (perhaps 1800 BC) advanced a 95-year cycle to synchronize the motions of the sun and the moon.A text on Vedic astronomy that has been dated to 1350 BC, was written by Lagadha. In 500 AD, Aryabhata presented a mathematical system that took the earth to spin on its axis and considered the motions of the planets with respect to the sun (in other words it was heliocentric). His book, the Aryabhatya, presented astronomical and mathematical theories in which the Earth was taken to be spinning on its axis and the periods of the planets were given with respect to the sun. Aryabhata wrote that 1,582,237,500 rotations of the Earth equal 57,753,336 lunar orbits. This is an extremely accurate ratio of a fundamental astronomical ratio (1,582,237,500/57,753,336 = 27.3964693572), and is perhaps the oldest astronomical constant calculated to such accuracy.Brahmagupta (598-668) was the head of the astronomical observatory at Ujjain and during his tenure there wrote a text on astronomy, the Brahmasphutasiddhanta in 628.
Ref: Indian Astronomy
So I wouldn't be at all surprised to find some sites in India that fit what we're looking for. Perhaps the Kailasa temple in Ellora, India is one such place? Coordinates 20 01N, 75 10E. (2/9ths of 90 degrees)
